Ambition 1

One way of looking at lifespan inequality is to take the age at which 10 % of the 50+ year-olds are expected to die in a given calendar year. To calculate that, we use lifetable distributions of lifespans after age 50. As an example, in Fig. 1 we show the Danish and Swedish populations. As indicated in the figure, the age above 50 by which the lifespans of the least-fortunate 10% are cut short are age 66 in Denmark today, age 61 in Denmark in 1960, and age 69 in Sweden today. We will do these and similar calculations for males, females, and males and females combined for all available populations and years in the Human Mortality Database and study trajectories over time as well as making comparisons among countries at the same point in time.

Analyses of lifespan distributions, both by period and by cohort, are important for four reasons.

First, and most centrally in our research, differences among individuals in ages at death are a major social inequality. Indeed, inequality in the length of life is the most fundamental inequality because all other inequalities are conditional on being alive.

Second, given any specific pension policy, the distribution of lifespans determines how many will die before retirement, how many will die shortly after retirement, how many will survive many years afterward, and what the cost will be both in some year and in the future. The research proposed here does not consider specific pension policies and does not consider costs. It does, however, provide a framework for understanding lifespan distributions and various ways of summarizing lifespan inequalities.

Third, financial institutions manage pension accounts that in aggregate are very large: in Denmark the funds in these accounts are twice the GNP. To make decisions about how to invest the funds in different kinds of assets and how much to pay out to pensioners, the administrators of pension funds need information about lifespan distributions. The particular set of people covered by a fund might tend to live longer (or shorter) than the general population, but knowledge of the lifespans of the general population is a basic starting point for further analysis. Consideration of the expected length of life is insufficient: information is needed about how many lives will be shorter or longer and by how much. The framework we propose to develop for estimating and summarizing lifetime distributions will help improve decision-making by pension managers and hence benefit their clients—i.e., us.

Fourth, individuals make decisions that affect how they spend the time of their lives. They decide how much education (and further education) to pursue, how hard to work, how much to save, when to retire (if they can influence this), and how to allocate spending over the trajectory of their retirement years. Knowledge of the forecast distribution of lifespans for people in the same generation is crucial for such decision-making. Individuals who are healthier (or unhealthier) than the average person born at the same time can adjust the lifespan distribution. Most people find such analysis difficult or unpleasant, but they can be helped by advisors or by social policies that guide decisions (such as required pension savings). No one, however, can think cogently about such decisions without pertinent information about the distributions of lifespans (hence Ambition 1) and forecasts of these distributions (hence Ambitions 2 and 3).

Pension systems are under demographic stress in most European countries and many other countries around the world. Sooner or later pension policies will need to be substantially reformed (even more radically than to date) to guarantee future sustainability. In devising these reforms, considerations of fairness and of minimizing disparities are crucial. In particular, for the four reasons adumbrated above, analyses of lifespan distributions are essential. Some analyses have been and are being undertaken to compare SES among subpopulations. Research on and discussion of individual lifespan inequalities, however, have been neglected. Consider a simple example. The economic sustainability of a pension system might be achieved by increasing the standard pension age to 80. This, however, would result in egregious inequalities in chances of reaching retirement.

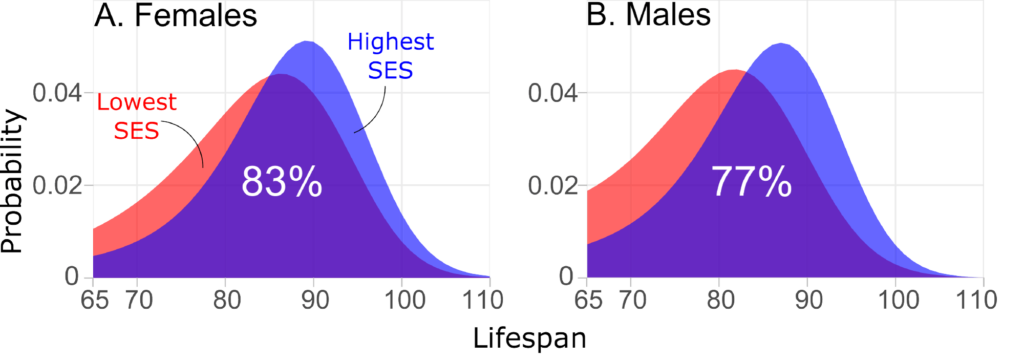
A key reason to supplement analyses of SES inequalities in lifespans with analyses of individual inequalities is that there is so much overlap of SES groups. Figure 2 illustrates this with some Danish data. The overlap between the distributions of lifespans of the lowest vs. the highest SES quintiles is 83% for females and 77% for males from the best-off group. Another way of summarizing this is to consider the following hypothetical experiment. Take a 65-year-old person at random from the most-disadvantaged group and take a 65-year-old at random for the best-off group. Using the appropriate Danish lifetable, randomly generate an age at death for each of these individuals. For 36% of such female and 30% of such male pairs, the person from the disadvantaged group will wind up living longer than the person from the advantaged subpopulation.

Considerations of individual lifespan inequality will not, by themselves, be decisive in debates about pension reform: such considerations will play a subsidiary role. But they should play a bigger role than currently. Hence our bold but limited goal to add individual lifespan inequality to the list of perspectives policy analysts, policymakers and the public should consider. We want to open up a new horizon, an additional perspective. We plan to do so by publishing articles in high-impact journals, that is, by doing science and demonstrating that analysis of lifespan inequalities leads to new insights. We also plan to reach out to the public and to policymakers with help from Population Europe.